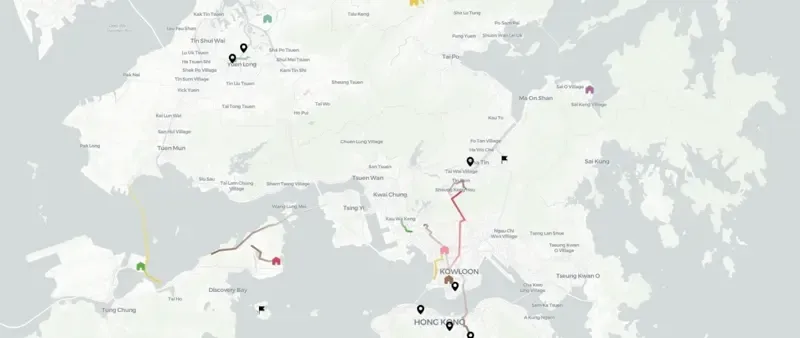
Routing Optimization using OR-Tools with Visualization

Brief description

Build a workflow in Python to solve daily scheduling problem with hundreds of daily vehicle requests
Conducted extensive literature reviews on mathematical programming and vehicle routing problem (VRP)
Applied constraint programming to solve VRP with time window and capacity constraints in Python using OR-Tools
Visualized geospatial data on map of Hong Kong interactively in JavaScript

It is a solver with visualization to solve Pickup Delivery Problem (PDP) with Time Windows, Capacity, Breaks and Priority Constraints for a transport company serving people with disabilities.

Design Document (Trimmed)

Introduction

This document describes the design of the routing optimization for a non-profit organization that provides transportation services for people with disabilities.

It does not describe the decision making of the business constraints such as maximum working hours and length of break time. Those constraints are assumed to be given by the organization as constants.

It is aimed at the following audiences:

data scientists
software engineers
project managers

Prerequisite: It is assumed that you understand python programming and basic concepts of routing optimization. If you are not familiar with the latter concept, please refer to the recommended readings section.

This app is similar to the Uber app, but it is designed for people with disabilities, and with much earlier scheduling, and much more complex constraints.

After reading this document, you are expected to know the goals, objectives, assumptions, and constraints of the routing optimization. You will also know how to run, maintain, and improve the program.

Background

The company provides a point-to-point service that allows passengers to book a ride up to 4 days in advance, which allows ride sharing. The company needs to digest 500 daily requests with 200 vehicles. 40 of them are often in stand-by or maintenance modes. The vehicles would be stating or ending at 17 depots, which are spread around Hong Kong. The company also hired around 180 drivers, while some of them are part-time drivers.

Methodology

It is just a vehicle routing problem (VRP) with pickup and delivery, time windows, capacity, breaks, and priority constraints. It is often termed as the Vehicle Routing Problem (VRP), Pickup and Delivery Problem (PDP), or Dial-a-Ride Problem (DARP) in academic literature. It is a well-known problem with well-established frameworks and tools to solve it. The problem is mainly framed in two paradigms, which are mixed integer linear programming (MILP) and constraint programming (CP). The former is more suitable for small to medium size problems, while the latter is more suitable for medium to large size problems with complex constraints.

The most difficult part is to define the constraints in mathematical terms to be plugged into a mathematical model, and the rest is just a matter of choosing a well-developed optimization algorithm from a well-established optimization software to get an acceptable solution with low cost according to the objective in a limited time.

Since the company has to deal with 500 daily requests in average in a complex setting according to business needs, constraint programming is chosen to solve the problem due to its speed and generality. The optimization software used in this project is OR-Tools, a Google’s open-source optimization software that is free to use. It also has a dedicated routing module that is designed to solve VRP in constraint programming, with a good documentation, lots of awards, and a great community support. To know more about OR-Tools, please refer to the recommended readings section.

Goals and Objectives

Goals

檢視固定路線服務的現行路線編訂
- 增加固定路線服務用戶和乘客人次
- 減少固定路線輪候名單申請人數目
提高點到點電話預約服務的車輛的使用率
檢討載客量低的聯載服務路線

Objectives

提高每天總載客量
減少每天總行車距離
減少每天用車數目
減少每天用車要求拒絕率

Input Data Requirement

Every row of the input data represents a request for a trip. The data includes the following columns:

date: date of the trip
boardTime: the time when the passenger boards the vehicle
boardlng: longitude of the boarding location
boardlat: latitude of the boarding location
alightTime: the time when the passenger alights the vehicle
alightlng: longitude of the alighting location
alightlat: latitude of the alighting location
wheelchair: whether the passenger is a wheelchair user
passenger: the number of normal passengers
partner_cnt: the number of partners
purpose: the purpose of the trip

Technical Details of OR-Tools Model

NOTE: Read it only if you are needed to tune the model. Otherwise, you can skip this section.

Time Variables

Variables

Arrival Time - CumulVar
Waiting Time - SlackVar
Transit
DepartureTime

Transformation equations

ArrivalTime(B) = ArrivalTime(A) + Transit(A, B) + WaitingTime(A) and
Transit(A, B) == ServiceTime(A) + TravelTime(A,B) == TotalTime(A,B)
so DepartureTime(A) = ArrivalTime(A) + ServiceTime(A) + WaitingTime(A)

References

Objective function

Try to minimize the costs
It doesn’t mean the standard deviation is minimized
Without setting a proper cost, it returns any route that fit the hard constraints
ref
maximizing seems doable

Type of costs

dimension.SetSpanCostCoefficientForAllVehicles(coeff)
- one coefficient per vehicle, default 0
- useful for dimension other than time because there is already arc cost for time
- add span cost on time_dimension, even if the coefficient is one, might kill the performance of the solver, making it stuck in local minimum or returning no solution
GlobalSpanCost
- one coefficient per dimension, default 0
- it minimizes the difference between max and min along the entire plan
- e.g. [6, 0, 0] == [6, 6, 0]
- explanation with calculation
ArcCost
- one coefficient per arc, default 0
- to be used by any initial first strategy
- Would be used in the objective function
- only one arc cost are allowed across all dimensions
FixedChostOfVehicle
- one cost per vehicle, default 0
DisjuctionPenaltyCost
- imposed by AddDisjunction
- added to objective function once a node is dropped
- default all nodes are mandatory, i.e. INFINITE COST
SoftConstraintPenaltyCost
- imposed by SoftUpperBOund or SoftLowerBound
- added to objective function once a soft constraint is violated
- default only hard limit
routing.SetAmortizedCostFactorsOfAllVehicles(100, 100)
- reduce number of used vehicles if possible by first term
- aims at making the routes as dense as possible by second term
- code ref
- it seems produce no difference while making the objective value being negative

How to add a reward?

Considering the followings as rewards are good

number of served wheelchairs
number of served normal passengers

First solution strategy

ALL_UNPERFORMED, GLOBAL_CHEAPEST_ARC are good methods for models with many constraints because they will find a feasible solution in seconds, then heuristics could quickly react to remove the penalties. Other methods may struggle to find a feasible solution even in 10 minutes.

PDP constraints

It can be done by adding routing.AddPickupAndDelivery, with two additional constraints that restrict the vehicle to be the same for both pickup and delivery, and the delivery time to be later than the pickup time. The code snippet is as follows:

def add_pickups_deliveries_constraint(routing, manager, data, time_dimension):
    # Define Transportation Requests.
    for request in data.pickups_deliveries:
        pickup_index = manager.NodeToIndex(request[0])
        delivery_index = manager.NodeToIndex(request[1])
        routing.AddPickupAndDelivery(pickup_index, delivery_index)
        # Same vehicle should perform pickup and delivery.
        routing.solver().Add(
            routing.VehicleVar(pickup_index) == routing.VehicleVar(delivery_index)
        )
        # delivery should be later than pickup.
        routing.solver().Add(
            time_dimension.CumulVar(pickup_index)
            <= time_dimension.CumulVar(delivery_index)
        )

Other potential useful constraints that are not yet used

routing.AddPickupAndDeliverySets
routing.SetPickupToDeliveryLimitFunctionForPair

Break Time

To impose a break interval, we can do it easily with the following methods:

time_dimension.CumulVar(index).RemoveInterval(A, B)
FixedDurationIntervalVar and SetBreakIntervalsOfVehicle

However, break constraint itself has no information about capacity/load dimension. If break is imposed without additional constraint linking break and capacity, the vehicle might take a break with passengers riding on it, which is not acceptable solution. So, a additional constraint should be added to avoid this. ref

Current solution

To make sure that the break is not in between pickup and delivery, we can impose a travel time constraint between pickup and delivery, making sure that the delivery time minus the pickup time, i.e. the actual travel time, shall not be greater than direct travel time plus break time. So that no break could be inserted in between. The code snippet is as follows:

for request in data["pickups_deliveries"]:
    pickup_index = manager.NodeToIndex(request[0])
    delivery_index = manager.NodeToIndex(request[1])
    time_callback = create_time_evaluator(data, manager)
    overall_travel_time = time_callback(pickup_index, delivery_index)
    routing.solver().Add(
        time_dimension.CumulVar(delivery_index)
        - time_dimension.CumulVar(pickup_index)
        <= (BREAK_TIME - 1) + int(overall_travel_time)
    )

Some readings to enhance the understanding of break time

Potential solutions
Some discussions
- https://github.com/google/or-tools/issues/1202
- https://github.com/google/or-tools/discussions/2693

Priority Constraint

Current solution

Add routing.AddDisjunction with a much higher cost compared to the other nodes with lower priority

Alternatives

Don’t add routing.AddDisjunction on high priority nodes
1. NOTE: it is likely that the solver will become unfeasible
Add a penalty to the start-time of a priority job
Find solution for high priority nodes first
SetCumulVarSoftUpperBOund

How to model shift?

There can only be n (180) vehicles outside the depot simultaneously
There are limited vehicles at each depot
There are limited driving for each driver
There are limited working hours, including waiting time for each driver
The waiting time and shifting time are counted in slack time, using the same vehicle for different drivers, it may result in a violation of the working hours, but actually not.

multi trip reload depot

So, using the same vehicle for different drivers will violate the working hours and driving hours. While using different vehicles for different drivers will violate the number of concurrent vehicles outside the depot constraint, and violate the number of vehicles at each depot constraint.

Could i reset the duration of the vehicle to 0 after each shift? ref

How to add back the dropped disjunct node?

NOTE: if there are unused vehicles and dropped nodes co-existing, it is likely that the imposed assumptions are incorrect, such that the requests are infeasible to be served by any vehicle. E.g. exceeding seat demand, exceeding estimated travel time compared to allowed travel time derived from time window, etc.

Ideas

References

Armbrust, Philipp, Philipp Hungerländer, Kerstin Maier, and Veronika Pachatz. “Case Study of Dial-a-Ride Problems Arising in Austrian Rural Regions.” Transportation Research Procedia 62 (2022): 197–204. https://doi.org/10.1016/j.trpro.2022.02.025.
Baita, F., R. Pesenti, W. Ukovich, and D. Favaretto. “A Comparison of Different Solution Approaches to the Vehicle Scheduling Problem in a Practical Case.” Computers & Operations Research 27, no. 13 (November 2000): 1249–69. https://doi.org/10.1016/S0305-0548(99)00073-8.
Brandão, José, and Alan Mercer. “A Tabu Search Algorithm for the Multi-Trip Vehicle Routing and Scheduling Problem.” European Journal of Operational Research 100, no. 1 (July 1997): 180–91. https://doi.org/10.1016/S0377-2217(97)00010-6.
Bunte, Stefan, and Natalia Kliewer. “An Overview on Vehicle Scheduling Models.” Public Transport 1, no. 4 (November 2009): 299–317. https://doi.org/10.1007/s12469-010-0018-5.
Cordeau, Jean-François, and Gilbert Laporte. “The Dial-a-Ride Problem: Models and Algorithms.” Annals of Operations Research 153, no. 1 (June 6, 2007): 29–46. https://doi.org/10.1007/s10479-007-0170-8.
Dong, Sharon. “New Formulations and Solution Methods for the Dial-a-Ride Problem.” UNSW Sydney, 2022. https://doi.org/10.26190/UNSWORKS/24100.
Foster, B. A., and D. M. Ryan. “An Integer Programming Approach to the Vehicle Scheduling Problem.” Operational Research Quarterly (1970-1977) 27, no. 2 (1976): 367. https://doi.org/10.2307/3009018.
Gaul, Daniela, Kathrin Klamroth, and Michael Stiglmayr. “Solving the Dynamic Dial-a-Ride Problem Using a Rolling-Horizon Event-Based Graph.” Application/pdf. OASIcs, Volume 96, ATMOS 2021 96 (2021): 8:1-8:16. https://doi.org/10.4230/OASICS.ATMOS.2021.8.
Gkiotsalitis, K., and A. Nikolopoulou. “The Multi-Vehicle Dial-a-Ride Problem with Interchange and Perceived Passenger Travel Times.” Transportation Research Part C: Emerging Technologies 156 (November 2023): 104353. https://doi.org/10.1016/j.trc.2023.104353.
Haghani, Ali, Mohamadreza Banihashemi, and Kun-Hung Chiang. “A Comparative Analysis of Bus Transit Vehicle Scheduling Models.” Transportation Research Part B: Methodological 37, no. 4 (May 2003): 301–22. https://doi.org/10.1016/S0191-2615(02)00007-3.
Häll, Carl H., Henrik Andersson, Jan T. Lundgren, and Peter Värbrand. “The Integrated Dial-a-Ride Problem.” Public Transport 1, no. 1 (May 2009): 39–54. https://doi.org/10.1007/s12469-008-0006-1.
Hassold, Stephan, and Avishai (Avi) Ceder. “Public Transport Vehicle Scheduling Featuring Multiple Vehicle Types.” Transportation Research Part B: Methodological 67 (September 2014): 129–43. https://doi.org/10.1016/j.trb.2014.04.009.
Hill, Arthur V., and W. C. Benton. “Modelling Intra-City Time-Dependent Travel Speeds for Vehicle Scheduling Problems.” Journal of the Operational Research Society 43, no. 4 (April 1992): 343–51. https://doi.org/10.1057/jors.1992.49.
Ho, Sin C., W.Y. Szeto, Yong-Hong Kuo, Janny M.Y. Leung, Matthew Petering, and Terence W.H. Tou. “A Survey of Dial-a-Ride Problems: Literature Review and Recent Developments.” Transportation Research Part B: Methodological 111 (May 2018): 395–421. https://doi.org/10.1016/j.trb.2018.02.001.
Hungerländer, Philipp, Kerstin Maier, Veronika Pachatz, and Christian Truden. “Improving Sharing Rates of a Dial-a-Ride Problem Implemented for an Austrian Mobility Provider.” Transportation Research Procedia 52 (2021): 525–32. https://doi.org/10.1016/j.trpro.2021.01.062.
Johnsen, Lennart C., and Frank Meisel. “Interrelated Trips in the Rural Dial-a-Ride Problem with Autonomous Vehicles.” European Journal of Operational Research 303, no. 1 (November 2022): 201–19. https://doi.org/10.1016/j.ejor.2022.02.021.
Liang, Xiao, Gonçalo Homem De Almeida Correia, Kun An, and Bart Van Arem. “Automated Taxis’ Dial-a-Ride Problem with Ride-Sharing Considering Congestion-Based Dynamic Travel Times.” Transportation Research Part C: Emerging Technologies 112 (March 2020): 260–81. https://doi.org/10.1016/j.trc.2020.01.024.
Lim, Andrew, Zhenzhen Zhang, and Hu Qin. “Pickup and Delivery Service with Manpower Planning in Hong Kong Public Hospitals.” Transportation Science 51, no. 2 (May 2017): 688–705. https://doi.org/10.1287/trsc.2015.0611.
Malheiros, Igor, Rodrigo Ramalho, Bruno Passeti, Teobaldo Bulhões, and Anand Subramanian. “A Hybrid Algorithm for the Multi-Depot Heterogeneous Dial-a-Ride Problem.” Computers & Operations Research 129 (May 2021): 105196. https://doi.org/10.1016/j.cor.2020.105196.
Masson, Renaud, Fabien Lehuédé, and Olivier Péton. “The Dial-A-Ride Problem with Transfers.” Computers & Operations Research 41 (January 2014): 12–23. https://doi.org/10.1016/j.cor.2013.07.020.
Molenbruch, Yves, Kris Braekers, and An Caris. “Typology and Literature Review for Dial-a-Ride Problems.” Annals of Operations Research 259, no. 1–2 (December 2017): 295–325. https://doi.org/10.1007/s10479-017-2525-0.
Molenbruch, Yves, Kris Braekers, An Caris, and Greet Vanden Berghe. “Multi-Directional Local Search for a Bi-Objective Dial-a-Ride Problem in Patient Transportation.” Computers & Operations Research 77 (January 2017): 58–71. https://doi.org/10.1016/j.cor.2016.07.020.
Parragh, Sophie N., Jorge Pinho De Sousa, and Bernardo Almada-Lobo. “The Dial-a-Ride Problem with Split Requests and Profits.” Transportation Science 49, no. 2 (May 2015): 311–34. https://doi.org/10.1287/trsc.2014.0520.
Pfeiffer, Christian, and Arne Schulz. “An ALNS Algorithm for the Static Dial-a-Ride Problem with Ride and Waiting Time Minimization.” OR Spectrum 44, no. 1 (March 2022): 87–119. https://doi.org/10.1007/s00291-021-00656-7.
Posada, Marcus, Henrik Andersson, and Carl H. Häll. “The Integrated Dial-a-Ride Problem with Timetabled Fixed Route Service.” Public Transport 9, no. 1–2 (July 2017): 217–41. https://doi.org/10.1007/s12469-016-0128-9.
Rist, Yannik, and Michael A. Forbes. “A New Formulation for the Dial-a-Ride Problem.” Transportation Science 55, no. 5 (September 2021): 1113–35. https://doi.org/10.1287/trsc.2021.1044.
Ritzinger, Ulrike, Jakob Puchinger, Christian Rudloff, and Richard F. Hartl. “Comparison of Anticipatory Algorithms for a Dial-a-Ride Problem.” European Journal of Operational Research 301, no. 2 (September 2022): 591–608. https://doi.org/10.1016/j.ejor.2021.10.060.
Schulz, Arne, and Christian Pfeiffer. “A Branch-and-Cut Algorithm for the Dial-a-Ride Problem with Incompatible Customer Types.” Transportation Research Part E: Logistics and Transportation Review 181 (January 2024): 103394. https://doi.org/10.1016/j.tre.2023.103394.
Sharif Azadeh, Sh., Bilge Atasoy, Moshe E. Ben-Akiva, M. Bierlaire, and M.Y. Maknoon. “Choice-Driven Dial-a-Ride Problem for Demand Responsive Mobility Service.” Transportation Research Part B: Methodological 161 (July 2022): 128–49. https://doi.org/10.1016/j.trb.2022.04.008.
Su, Yue, Nicolas Dupin, and Jakob Puchinger. “A Deterministic Annealing Local Search for the Electric Autonomous Dial-a-Ride Problem.” European Journal of Operational Research 309, no. 3 (September 2023): 1091–1111. https://doi.org/10.1016/j.ejor.2023.02.012.
Vallee, S., A. Oulamara, and W. Ramdane Cherif-Khettaf. “New Online Reinsertion Approaches for a Dynamic Dial-a-Ride Problem.” Journal of Computational Science 47 (November 2020): 101199. https://doi.org/10.1016/j.jocs.2020.101199.
Wassan, Naveed, Niaz Wassan, Gábor Nagy, and Saïd Salhi. “The Multiple Trip Vehicle Routing Problem with Backhauls: Formulation and a Two-Level Variable Neighbourhood Search.” Computers & Operations Research 78 (February 2017): 454–67. https://doi.org/10.1016/j.cor.2015.12.017.
Yao, Enjian, Tong Liu, Tianwei Lu, and Yang Yang. “Optimization of Electric Vehicle Scheduling with Multiple Vehicle Types in Public Transport.” Sustainable Cities and Society 52 (January 2020): 101862. https://doi.org/10.1016/j.scs.2019.101862.
Zhang, Zhenzhen, Mengyang Liu, and Andrew Lim. “A Memetic Algorithm for the Patient Transportation Problem.” Omega 54 (July 2015): 60–71. https://doi.org/10.1016/j.omega.2015.01.011.

Brief description

Design Document (Trimmed)

Introduction

Background

Methodology

Goals and Objectives

Input Data Requirement

Technical Details of OR-Tools Model

Time Variables

Objective function

First solution strategy

PDP constraints

Break Time

Priority Constraint

How to model shift?

How to add back the dropped disjunct node?

How to insert new request with existing solution?

Speed Optimization

How to make more log?

Recommended Readings

References